.
PRACTICA CON TU GUIA
Los estudiantes de cuarto grado estudiaron la metamorfosis de la rana. En clase la profesora les explicó que durante este proceso, la rana es un embrión por espacio de 7 días. Luego, dura 44 días siendo renacuajo. Finalmente, tarda 21 días en convertirse en una rana adulta.
Al calcular sumas podemos aplicar estas propiedades:
CONMUTATIVA: Esta propiedad nos dice que el orden de los sumandos no altera la suma. Ej.
Resuelve las operaciones de dos formas distintas.
4. Comunicación. Escribe la propiedad o propiedades aplicadas en cada caso.
* 25 + 63 = 63 + 25 = 88 …………………………………………………………………………………………
………………………………………………………..
5. Solución de problemas.
Observa el número de asistentes a un estadio de fútbol.
SUSTRACCIÓN DE NÚMEROS NATURALES
Ej. La semana pasada asistieron 9324 personas a un concierto. Si 3719 ocuparon la localidad de platea, ¿cuántas personas asistieron a los balcones?
PRACTICA CON TU AYUDANTE
Un alpinista desea subir a la cima de una montaña que tiene 1250 metros de altura. Su plan indica que subirá 468 metros en la primera etapa, 350 en la segunda y el resto en la tercera. Calcula los metros que le faltan para llegar a la cima después de la primera etapa. ….Realiza la operación y escribe la respuesta. Haz uso de tu cuaderno
El dato que más se repite se llama MODA
Lea detenidamente la siguiente inquietud
GRADO: CUARTO. 1- 2- 3.
PROPÓSITOS DE APRENDIZAJE.
Es importante que para el desarrollo de esta guía tengan a la mano el transportador, escuadra, regla o si no cuenta con estos juegos geométricos puede utilizar cualquier utensilio como una varita, un palito, una pita, etc. que lo tome como referencia de medidas.
Sé lo creativo que ustedes son. ¡Ánimo!
No olvides que debes hacer buen manejo con la regla.
Si puedes ver el siguiente link, lo puedes aprovechar para enriquecer tus aprendizajes:
DETENER LA PROPAGACIÓN
DEL COVID 19 ES UN COMPROMISO DE TODOS
|
|
GUÍA DE TRABAJO EN
CASA
Área y/o asignatura: ARITMÉTICA
Grado: 4 Curso: 1 – 2 -
3 Período Académico: II
FECHA: MAYO 18 a MAYO 29/ 2020
DOCENTES: ELIZABETH NAVARRO
NOMBRE DE LA UNIDAD: NÚMEROS NATURALES
|
|
Propósitos
de aprendizajes:
FACILITAR AL ESTUDIANTE EL CONOCIMIENTO SOBRE EL PROCESO DE LA MULTIPLICACIÓN PARA REALIZAR LAS OPERACIONES DE MANERA RÁPIDA Y APLICARLA EN SU CONTEXTO DEL DÍA A DÍA.
|
Contenidos temáticos:
MULTIPLICACIÓN DE NÚMEROS NATURALES
.
PROPIEDADES DE LA MULTIPLICACIÓN
MULTIPLICACIÓN DE FACTORES TERMINADOS EN CERO
|
Te recomiendo que una vez hayas terminado de elaborar toda estas actividades. Pídele a tu acompañante en esta tarea que verifique que lo que hayas realizado lo sepas hacer de una forma excelente. Si vez que te falta algo por aprender vuelves nuevamente a revisar los conceptos.
DETENER LA PROPAGACIÓN
DEL COVID 19 ES UN COMPROMISO DE TODOS
|
|
GUÍA DE TRABAJO EN
CASA
Área y/o asignatura: GEOMETRÍA Grado: 4 Curso: 1 – 2 - 3 Período
Académico: II
FECHA: MAYO 18 a MAYO 29/ 2020
DOCENTES: ELIZABETH NAVARRO
NOMBRE DE LA UNIDAD: IDENTIFICO FIGURAS CUADRILÁTEROS
|
|
Propósitos
de aprendizajes:
EL
ESTUDIANTE IDENTIFIQUE FORMAS GEOMÉTRICAS DE SU ENTORNO.
|
Contenidos temáticos:
CUADRILÁTEROS Y SU CLASIFICACIÓN
|
DETENER LA PROPAGACIÓN
DEL COVID 19 ES UN COMPROMISO DE TODOS
|
|
GUÍA DE TRABAJO EN
CASA
Área y/o asignatura: ESTADÍSTICA Grado: 4 Curso: 1 – 2 - 3 Período
Académico: II
FECHA: MAYO 18 a MAYO 29/ 2020
DOCENTES: ELIZABETH NAVARRO
NOMBRE DE LA UNIDAD: ESTUDIO ESTADÍSTICO
|
|
Propósitos
de aprendizajes:
EL
ESTUDIANTE INTERPRETA LECTURA EN GRÁFICAS DE LINEAS.
|
Contenidos temáticos:
GRÁFICAS DE LINEA
|
|
DETENER
LA PROPAGACIÓN DEL COVID 19 ES UN COMPROMISO DE TODOS |
|
|
GUIA
DE TRABAJO EN CASA Área y/o
asignatura: ARITMETICA Grado: 4 Curso: 1 – 2 -3
Período Académico: II
FECHA: JUNIO 8 A JULIO 17 DOCENTES: ELIZABETH NAVARRO
NOMBRE DE LA UNIDAD:
OPERACIONES CON MUMEROS NATURALES
|
|
|
Propósitos
de aprendizajes:
RESOLVER
CUALQUIERA SITUACIÓN DE SU VIDA DIARIA EN DONDE TENGA QUE REPARTIR,
DISTRIBUIR, DIVIDIR, EN PARTES IGUALES.
HACIENDO
USO DE LAS TABLAS DE MULTIPLICAR RELIZAR UNA DIVISIÓN E IDENTIFICAR SI ES
EXACTA O INEXACTA
IDENTIFICAR
LOS MÚLTIPLOS Y DIVISORES DE UN NÚMERO
|
Contenidos
temáticos: DIVISION DE NÚMEROS
NATURALES DIVISIÓN EXACTA E
INEXACTA PRUEBA DE LA DIVISIÓN MULTPLOS Y DIVISORES
DE UN NÚMERO CRITERIOS DE
DIVISIBILIDAD
|
Mi querido estudiante;
cuenta conmigo, siempre estaré dispuesta a ayudarte y a escucharte.
Con cariño y aprecio,
Tu profesora. Elizabeth Navarro
MOMENTO
1: CONOCIMIENTOS PREVIOS
Cuando hemos cumplido
años y estamos en el colegio. Llevamos dulces para compartir la alegría que
sentimos por estar rodeados de nuestros compañeros que nos aprecian y nos
queremos. ANALIZA LA SIGUIENTE SITUACIÓN.
1. Ehimy nuestra
compañera llevó 2 bolsa de dulces para compartir; cada bolsa tiene 50 confites
si en el grupo son 42 niños. ¿Cuántos confites le darían Ehimy a cada niña para
que tocaran iguales?
Desarrolla tu análisis
en el cuaderno. Te propongo ilustrar la situación planteada y luego resuelves
la operación que consideres te demuestre que Ehimy dio a cada uno de sus
compañeros.
2. Los Hermanos
Cabrales Pacheco deciden hacer una obra social para ayudar a diez niños que no
tienen para sus útiles y emprenden una campaña con el apoyo de sus padres. Al terminar
la campaña recogieron 250.000 (doscientos cincuenta mil pesos).
PIENSA UN MOMENTO. ¿Si lo que recogieron
alcanzo para comprar el valor de los útiles, Cuanto fue el valor para cada
niño? Realiza la operación en tu cuaderno de apuntes.
Seguramente has
realizado correctamente las respuestas a estas dos situaciones presentadas. Te
invito a que según tus posibilidades observes el siguiente video.
Recuerdas que debes
tener tus implementos necesarios como son: cuadernos de apuntes, implementos
geométricos, lápiz, colores y una buena disposición al trabajo.
https://www.youtube.com/watch?v=UHXwGxfTJIQ
Como te has dado cuenta
el tema que vamos a aprender es la división; que entre otras cosas no es nuevo
para ti. Espero no me falles en este aprendizaje.
MOMENTO
2: CONCEPTUALIZACIÓN
1. Tema # 1.
DIVISIÓN
DE NÚMEROS NATURALES
La división es una
operación de números naturales, que permite solucionar situaciones concretas
asociadas a la repartición equitativa o a la determinación del número de grupos
iguales que se pueden formar con una cantidad determinada
Los términos de una
división son dividendo, divisor, cociente y residuo.
Como lo habías
expresado en clases del año anterior; que el que se sabía las tablas de
multiplicar, sabía dividir, es el momento para que compruebes una vez más tus
propias conclusiones.
Te invito a que lo que
realices lo hagas con dedicación y mucha concentración. Ten presente que
siempre te estoy apoyando desde la distancia. Llámame cuando estés confundido.
A continuación,
identificarás los términos de la división con el siguiente ejemplo y te darás
cuenta cómo se va llevando a cabo el proceso de la división.
Lee con atención el
siguiente problema, te sirve de referencia para aplicar más adelante; si es
posible hazlo cuantas veces lo requieras hasta entenderlo. Los dibujos son muy
importantes.
Transcribe
de forma igual al cuaderno. Esto es fundamental en el proceso, para adquirir
habilidades en el desarrollo de cualquier problema que se te coloque y debas
hacerlo.
PRACTICA
EL SIGUIENTE EJERCICIO CON TU AYUDANTE
1. A una tienda de animales llegó un pedido de 380
peces los cuales serán organizados en acuarios de 12 peces.
·
¿Cuántos
acuarios necesitan?
·
Si los peces
se repartieron en 15 acuarios. ¿Cuántos peces quedarían en cada uno?
Te pido que representes los acuarios, y
coloques los peces que se te dice que tiene cada acuario, luego utilizas el
esquema de la división y terminar de efectuarla, allí tienes los espacios para
que coloques los números que corresponde.
Te
recuerdo si algo no entiendas por favor llámame, una video llamada, un audio
que me mandes o en los encuentros sincrónicos. No tengas pena en preguntar,
quizás otros también tengan tu inquietud.
MOMENTO
3. RESUELVE Y APLICA
ES IMPORTANTE EN ESTE
PROCESO QUE DESARROLLES TUS COMPETENCIAS.
2.
EJERCITACIÓN. Efectúa
las siguientes divisiones y señala los términos en cada una de ellas.
Realízalas
en el cuaderno.
·
702 entre 18
·
483 entre 3
·
1245 entre 5
·
5983 entre 24
·
45976 entre 39
3.
Pinta del mismo color los recuadros de las
divisiones que tengan el mismo cociente.
4.
MODELACIÓN. Plantea un
problema que requiera de la división y que contemple la información que te
suministro y lo resuelves en el cuaderno. Lo que quiero decirte es que inventes
un problema teniendo en cuenta la información que sigue.
530 viajes
con el cupo completo y 12720 viajeros
En este ejercicio debes
realizar un escrito con las condiciones dadas. ¡Animo!
SOLUCIÓN DE PROBLEMAS
5.
Un grupo de científicos repartirán 2970 gusanos
de seda en cajas de cartón con la misma cantidad.
·
¿Cuántas cajas necesitan si en cada una ponen
17 gusanos?
·
Si tienen 25 cajas, ¿cuántos gusanos deben
poner en cada caja?
ESTE PRIMER TEMA DEBES
DESARROLLARLO SEGÚN EL HORARIO DE CLASES EN 4 HORAS. (PRIMERA SEMANA)
2. Tema # 2.
DIVISIÓN
EXACTA E INEXACTA
Según los residuos que
se obtienen al calcular el cociente, las divisiones pueden ser exactas o inexactas
Una división es exacta
cuando su residuo es cero. Ej.
·
45 entre
5 es una división exacta; el cociente es 9 y el residuo es 0
Una división es
inexacta cuando su residuo no es cero. Ej.
·
172
entre 5 es una división inexacta; el cociente es 34 y el residuo es 2.
ES IMPORTANTE QUE
TENGAS CLARO CUALES SON LOS TERMINOS DE LA DIVISIÓN.
Te proporciono el
siguiente ejemplo y te invito a que lo practiques hasta comprenderlo.
R/ Juana durará 6 años y 3 meses pagando el crédito de su carro
Según tus posibilidades
te propongo el siguiente link
https://www.youtube.com/watch?v=KPub-RIh_dI
PRACTICA CON TU
AYUDANTE.
1.
El hecho de que haya
residuo indica que es necesario contratar un bus más para llevar a
esas………………personas.
Se deben
contratar……………………buses
RECUERDA QUE TU TIENES
GRANDES CAPACIDADES Y DEBES DAR A CONOCER TUS COMPETENCIAS. PARA ESTO TE
PROPONGO LOS SIGUIENTES EJERCICIOS.
2.
EJERCITACION. Realiza cada división en el
cuaderno. Indica cuáles son exactas y cuáles inexactas.
3.
Colorea
las casillas que tengan el cociente y el residuo de cada división. Realiza los
cálculos necesarios en el cuaderno.
En una división exacta, el cociente es 234 y el divisor es 13. ¿Cuál es el dividendo? Te oriento para esto. Debes multiplicar el cociente con el divisor. Resuélvelo y luego realizas la división; para que lo compruebes.
5.
Completa
la siguiente tabla. Ten en cuenta el procedimiento utilizado en el ejercicio
anterior.
SOLUCION
DE PROBLEMAS
6.
Una
barca transporta pasajeros de una orilla del río a otra. En cada viaje lleva 25
personas. ¿Cuántos viajes debe hacer para transportar a 400 pasajeros? ¿Y si se
suman 30 a los 400 pasajeros? ¿Y si llegan 50 personas más?
Si te
sientes con dificultad te agradezco una llamadita. Te recomiendo hacer los
dibujos eso te ayudará mucho´
ESTE SEGUNDO
TEMA DEBES DESARROLLARLO EN LA SEGUNDA SEMANA. FIJESE QUE TIENES MUCHO
EJERCICIOS PARA HACER.
Tema # 3.
PRUEBA DE LA DIVISIÓN
En el tema
anterior pudiste darte cuenta como es de fácil saber si una división está bien
hecha; sin embargo en este tema quedará bien claro este proceso. Ten presente
lo siguiente:
Cuando se
quiere realizar la prueba de la división se debe multiplicar el divisor por el
cociente y sumar el residuo. Si el resultado es igual al dividendo la división
es correcta.
En una
división bien hecha, siempre se cumple que:
Dividendo =
(divisor X cociente) + residuo
D = (d X c) + r
PRÁCTICA
CON TU AYUDANTE
1.
DESARROLLA
TUS COMPETENCIAS
2. EJERCITACIÓN. Utiliza la prueba de
la división para saber si esta división está bien hechas. Corrígela en caso
contrario.
|
Dividendo |
Divisor |
Cociente |
Residuo |
|
7405 |
79 |
93 |
58 |
|
1046 |
23 |
45 |
8 |
|
9654 |
17 |
567 |
18 |
3. COMUNICACIÓN.
En una división el dividendo es 716, el cociente es 88 y el residuo es 12. Si
el divisor es 8, ¿por qué la división está mal hecha? Justifica tu respuesta
Es fácil,
haz la división y tendrás fundamento para justificar.
Ayúdate con este video
que recoge todo lo que has estudiado hasta el momento. Si tienes la oportunidad
de verlo hazlo. https://www.youtube.com/watch?v=h_izOoVVeko
SOLUCIÓN
DE PROBLEMAS
4. Se repartieron 355 flores en seis jarrones. En
el reparto sobró una flor y en cada jarrón se colocaron 59 flores. Expresa
cuáles de esas cantidades son el dividendo, el divisor, el cociente y el
residuo. Aplica la prueba de la división para comprobar si el reparto está bien
hecho.
Tema
# 4.
MULTIPLOS
Y DIVISORES DE UN NÚMERO
Como has venido viendo lo importante de
la división es saber las tablas de multiplicar. Seguidamente vas a obtener un
nuevo conocimiento en este tema
Los múltiplos de un número son todos los
productos que se obtienen de multiplicarlo por 0, 1, 2, 3, 4, 5, 6, 7…
El conjunto de los MÚLTIPLOS de un número es INFINITO
Los divisores de un número son todos
aquellos que lo dividen exactamente.
El conjunto de los DIVISORES de un número es FINITO.
Antes de continuar ayúdate con el siguiente
video: https://www.youtube.com/watch?v=s72ZMDs99zk
Leer y releer el
siguiente ejercicio; para que luego desarrolles los siguientes:
Mario tiene en su
computador doce documentos que quiere guardar en carpetas con igual cantidad de
documentos. ¿De cuántas formas diferentes puede hacerlo?
Para responder se
hallan los divisores de 12
12 entre 1 =
12 ----------------------Una carpeta con doce archivos
12 entre 2 =
6 -----------------------Dos carpetas
con seis archivos
12 entre 3 =
4 ------------------------Tres carpetas con cuatro archivos
12 entre 4 =
3 ------------------------Cuatro carpetas con tres archivos
12 entre 6 =
2 -------------------------Seis carpetas con dos archivos
12 entre 12
= 1 ------------------------Doce carpetas con un archivo
Los números
anteriores son los divisores de 12. Los Divisores de 12 ={1, 2, 3, 4, 6, 12}
R/ Mario
puede organizar sus archivos de seis formas diferentes.
Vas a
realizar el siguiente ejercicio siguiendo el ejemplo anterior.
Practica con tu ayudante
1.
Encuentra los divisores de 36. Busca, en orden,
las parejas de números que al multiplicarse den como resultado 36.
1
X__________= 36
2
X__________= 36
3
X 12 = 36
_____X 9
= 36
6
X _________ = 36
Los divisores de 36 son = {1, 2, 3, ____,6, 9, 12, _____, _____}
2.
Encuentra los cinco primeros múltiplos de 7.
Multiplica el 7 por los cinco primeros números naturales.
0
X 7 =_______
_____X 7 =_______
_____X 7 =_______
3 X 7 =_______
_____X 7 = 28
Los múltiplos de 7 son = {____, 7, _____, _____,28, ____}
DESARROLLA
TUS COMPETENCIAS
3.
EJERCITACIÓN. Completa
la siguiente tabla
4.
RAZONAMIENTO. Encuentra
los divisores de 2, 3, 5, 7, y 11. ¿QUÉ CARACTERÍSTICAS TIENEN EN COMÚN?
Escribe verdadero o falso. Justifica tus respuestas.
( ) El 1 es múltiplo de todos los números
(
) El 1 es divisor de todos los números
SOLUCIÓN
DE PROBLEMAS
5.
Un zoológico adquirió 30 aves. Si se desea
poner el mismo número de aves en cada jaula, ¿Cuántas aves se necesitarán?
¿Cuántas aves caben en cada jaula? ¿Cuántas respuestas diferentes hallaste?
Te
sugiero para el desarrollo de este problema, hagas el dibujo representativo de
lo que se te pide; debes ser analítico y creativo; después haces las
operaciones.
Te recuerdo pasar todo
al cuaderno bien organizado; letra legible con su respectiva ortografía
correcta.
Tema
# 5
CRITERIOS
DE DIVISIBILIDAD
Un número es divisible
por otro si al realizar la división entre ellos el residuo es cero
Para determinar cuándo
un número es divisible por números menores que 10, se tienen en cuenta algunas
reglas o criterios como el siguiente.
·
Un número es divisible por 6 si es par y la
suma de sus cifras es múltiplo de 3.
·
32760 es divisible por 6 porque es par y la
suma de sus cifras (3 + 2 + 7 + 6 + 0) = 18 y 18 es múltiplo de 3.
Observa el siguiente
video te ayudará a terminar de comprender lo que sigue. Únete al siguiente link:
https://www.youtube.com/watch?v=9OAzUJD8Yr0
A continuación leer el
siguiente ejercicio. Leerlo varias veces te ayudará a entenderlo.
La profesora de
Ciencias organizó a sus 30 estudiantes en grupos con el mismo número de
integrantes. ¿De cuántas maneras distintas pudo hacerlo?
·
Para buscar las distintas maneras de organizar
los grupos se buscan los divisores de 30 o se tiene en cuenta los criterios de
divisibilidad.
Te ayudas
con tu orientador en casa; para desarrollar el siguiente ejercicio:
Oscar quiere
envasar 345 litros de jugo en botellas
·
¿Puede envasar el jugo en botellas de 2 litros?
R/___________se
puede envasar el jugo en botellas de 2 litros.
*¿345 es
número par? Sí_________ No_________
*¿Puede
envasar el jugo en botellas de 3 litros?
3 + 4 + 5 =___________
R/
___________se puede envasar el jugo en botellas de 3 litros
*¿De qué
otras maneras puede envasar el jugo?
Responde en
tu cuaderno. Animo te invito a demostrar tus capacidades y potencialidades que
Dios te ha dado.
3.
EJERCITACIÓN. Completa la
tabla.
|
Número |
Divisible por |
||||||
|
2 |
3 |
4 |
5 |
6 |
9 |
10 |
|
|
450 |
|
|
|
|
|
|
|
|
9198 |
|
|
|
|
|
|
|
|
6570 |
|
|
|
|
|
|
|
|
8871 |
|
|
|
|
|
|
|
4.
COMUNICACIÓN. Encuentra
el número que cumpla con las condiciones dadas.
·
Tienes tres cifras y es divisible por 5
·
Es mayor que 345 y menor que 380.Es divisible
por 3 y la suma de sus cifras es 18
SOLUCIÓN DE PROBLEMAS
5.
En una campaña de reforestación se quiere
sembrar 64 árboles en grupos con igual número de árboles.
·
¿Es posible armar cuatro grupos?
·
¿Es posible armar seis grupos?
TE PUEDES
AYUDAR, HACIENDO LOS DIBUJOS QUE TE PLANTEA EL PROBLEMA; PARA QUE PUEDAS
COMPRENDERLO Y DAR RESPUESTAS. REALIZA LAS OPERACIONES.
NOTA: AL FINALIZAR CADA
SEMANA RECIBO LAS RESPUESTA DE CADA GUÍA. LES RECUERDO QUE SON 5 SEMANAS PARA
ESTE TRABAJO.
AUTOEVALUACION
Después de terminar el estudio con estas guías, realiza las
siguientes preguntas. Se sincero consigo mismo
1. ¿Fue
claro y entendible el contenido en cada tema? _________________________
2. ¿Los
ejemplos que se proporcionaron y los videos fueron claros para ayudarte a
desarrollar los ejercicios propuestos? ________________________________________
3. ¿Necesitaste
pedir ayuda para resolver los ejercicios que se te propusieron? __________________________________________________________
4. ¿En
cuál de los temas consideras que te fueron fácil y entendible? ___________________________________________________________
5. En
cual o cuales ejercicios te fueron difíciles y aún no has entendido.
___________________________________________________________________
|
DETENER LA PROPAGACIÓN DEL COVID 19 ES UN
COMPROMISO DE TODOS |
|
|
GUIA
DE TRABAJO EN CASA
Área y/o asignatura: GEOMETRIA Grado: 4 Curso: 1 – 2 -3 Período Académico: II
FECHA: JUNIO 8 A JULIO17 DOCENTES:
ELIZABETH NAVARRO
NOMBRE DE LA UNIDAD:
SOLIDOS GEOMETRICOS
|
|
|
Propósitos
de aprendizajes:
IDENTIFICAR
COMO SE MUEVE LAS FIGURAS EN EL PLANO CARTESIANO REALIZAR
CÁLCULOS Y MEDICIONES DE FIGURAS EN SU CONTORNO
|
Contenidos
temáticos: COORDENADAS EN EL PLANO
CARTESIANO PERÍMETRO
|
MOMENTO
1. CONOCIMIENTOS PREVIOS
Haz escuchado alguna
vez las palabras Plano Cartesiano, perímetro y área.
Anota tu respuesta en tu cuaderno. Te recuerdo
que todo lo vas a realizar en el cuaderno NO en la guía.
No te preocupes si no
lo sabes lo vas a aprender en las siguientes guías.
Tema
# 1 COORDENADAS EN EL PLANO CARTESIANO
El plano cartesiano
permite realizar localizaciones exactas. Las coordenadas de un punto indican su
posición horizontal y vertical respecto al origen.
Te invito que veas el
siguiente video te ayudará a entender este tema. El link es https://www.youtube.com/watch?v=OcHxnc2j7to
Lo visto en el video es
lo mismo que a continuación vas a leer Hazlo con mucha concentración.
Silvia y sus amigos
participan en el juego de orientación organizado por el profesor de educación
física. Para superar las pruebas, deben localizar en un mapa los puestos de
control.
·
Para localizar el primer puesto de control, se
ubica en el plano cartesiano el punto de coordenadas (3, 4)
Practica y resuelve con
tu ayudante.
1.
Determine las coordenadas de los vértices del polígono
2.
EJERCITACION. Dibuja en
el cuaderno un plano cartesiano. Marca en cada caso los puntos. Únelos en el
orden dado.
*(1, 3); (3,
3); (4, 1); (5, 3); (7, 3); (6, 6); (7, 9); (5, 9); (4, 11); (3, 9); (1, 9);
(2, 6).
¿Cuántas
puntas tiene la estrella? _________________________
3.
COMUNICACIÓN:
Observa
el plano y contesta.
·
¿Qué hay en el punto (3,2)?
·
¿Y en el punto (1,5)?
·
¿En qué punto está ubicado el restaurante?
·
¿Qué encontramos en el punto (6,1)?
·
Si quiero una llamada telefónica, ¿a qué punto
me debo dirigir?
4.
RAZONAMIENTO.
Escribe
las coordenadas necesarias para dibujar la silueta del perro.
(__,__) (__,__) (__,__)
(__,__)
(__,__) (__,__) (__,__)
(__,__)
(__,__) (__,__) (__,__)
(__,__)
(__,__) (__,__) (__,__)
(__,__)
Tema #2 PERIMETRO
Alguna vez
has medido tu cuaderno de matemáticas. Si no lo has hecho hazlo. Mídelo por el
borde, utiliza una regla. ¿Cuánto mide?
Si puedes verte el siguiente video, hazlo. El
link es https://www.youtube.com/watch?v=ON1bheJhh1E
Como
aprenderás el perímetro de una figura es la medida de su borde.
COMPRENDE
Para conocer
el perímetro de un polígono cualquiera se deben medir y sumar las longitudes de
sus lados.
P=
2 cm + 3 cm + 4 cm
P= 9 cm
2 cm 4 cm
P= Perímetro
3 cm
Si los
polígonos son regulares, se mide el lado y se multiplica ese valor por su
número de lados.
2 cm P= lado X
números de lados
P= 2 cm X 6
P= 12 cm
PRACTICA Y RESUELVE CON TU AYUDANTE.
1.
Mide las longitudes de los lados de cada
polígono y calcula su perímetro
2.
RAZONAMIENTO. Deduce las
medidas que faltan en cada figura y
halla su perímetro.
3.
EJERCITACIÓN. Halla el
perímetro de:
·
El piso de la sala de tu casa o donde te ha
tocado pasar este aislamiento social.
4.
COMUNICACIÓN. Dibuja el
polígono que cumpla la condición dada.
·
Cuadrado de 16 centímetros (cm) de perímetro
·
Cuadrilátero de 36 cm de perímetro
·
Rectángulo de 18 cm de perímetro
SOLUCIÓN DE PROBLEMAS
5.
Una valla rectangular, cuyo lado más largo mide
12 metros (m) y es el doble del más corto, va a ser reforzada en su borde con
una lámina de metal. ¿Cuál es la medida de la lámina que se va a utilizar?
Acompáñate con el dibujo.
AUTOEVALUACIÓN
Después de terminar el estudio con estas guías, realiza las
siguientes preguntas. Se sincero consigo mismo
1. ¿Fue
claro y entendible el contenido en cada tema? _________________________
2. ¿Los
ejemplos que se proporcionaron y los videos fueron claros para ayudarte a
desarrollar los ejercicios propuestos? ________________________________________
3. ¿Necesitaste
pedir ayuda para resolver los ejercicios que se te propusieron? __________________________________________________________
4. ¿En
cuál de los temas consideras que te fueron fácil y entendible? ___________________________________________________________
5. En
cual o cuales ejercicios te fueron difíciles y aún no has entendido.
___________________________________________________________________
|
DETENER
LA PROPAGACIÓN DEL COVID 19 ES UN COMPROMISO DE TODOS |
|
|
GUIA
DE TRABAJO EN CASA Área y/o
asignatura: ESTADÍSTICA Grado:
4 Curso: 1 – 2 -3 Período
Académico: II
FECHA: JUNIO 8 A JULIO17 DOCENTES:
ELIZABETH NAVARRO
NOMBRE DE LA UNIDAD:
PROBABILIDAD
|
|
|
Propósitos
de aprendizajes:
Reconocer
que en el lanzamiento con dados al jugar se puede dar la probabilidad de ganar
Identificar
la secuencia que se tiene en ordenar números o figuras |
Contenidos
temáticos: NOCIONES DE
PROBABILIDAD SECUENCIAS Y
VARIACIÓN
|
SABERES
PREVIO.
¿Alguna vez has jugado
con dados? ¿Sabes cuánto puedes sacar al tirarlo?
¿Por qué crees que se puede
ganar una lotería? ¿Será que ya sabían el número? Responde en el cuaderno
Te invito a desarrollar
los siguientes ejercicios pero antes observa el video en el siguiente link https://www.youtube.com/watch?v=WeeEE8o1aqM
Tema # 1 PROBABILIDAD DE UN EVENTO
La probabilidad indica
la posibilidad de que ocurra un evento particular.
La probabilidad de que
ocurra un evento es la relación entre la cantidad de veces que sucede el caso
particular y el número total de casos posibles.
·
Al lanzar los dados 35 veces, el resultado 12
se obtuvo en cinco ocasiones. En este caso la posibilidad de obtener 12 fue 5
de 35.
Lee la
siguiente situación:
Para
celebrar su aniversario un hipermercado realizo un maratón de premios en el que
entrego un premio sorpresa por cada 100 clientes. Un cliente, seleccionado de
entre 100, debía sacar una boleta de una urna en la que había 10 balotas: 3
marcadas con electrodomésticos, 2 con dos viajes y 5 con aparatos para hacer
gimnasia.
·
El hecho de sacar una boleta de la urna se
llama EVENTO. En este caso, algunos
eventos tienen mayor probabilidad de ocurrir que otros.
·
La posibilidad de ocurrencia de un evento es la
PROBABILIDAD. La probabilidad de que
el ganador saque un electrodoméstico está determinada por la relación entre el
número de balotas marcadas con electrodomésticos y el número total de balotas
de la urna.
·
La probabilidad de ganar un viaje era 2 de 10 y
la de ganar un aparto de hacer gimnasia era de 5 de 10.
|
Total de balotas |
10 |
|
Balotas con
electrodomésticos |
3 |
|
Probabilidad |
3 de 10 |
Practica
con tu ayudante
1.
Dibuja la posibilidad que se tiene de obtener
los siguientes puntajes al lanzar dos dados.
·
5
·
6
·
7
·
12
2.
Calcula la probabilidad de cada evento.
·
Sacar, sin mirar, un color amarillo de tu
cartuchera
·
Sacar, sin mirar, una moneda de 200, en una
alcancía que tiene varias monedas de diferente valor.
3.
Describe una situación en la que la
probabilidad sea:
4 de 10
7
de 7
Solución
de problemas
4.
El carro del papá de Juliana tiene una placa
que termina en cifra par. Si las dos primeras cifras son 5 y 9, escribe los
posibles números que puede tener la placa del carro del papá de Juliana. Dibuja
las placas en el cuaderno.
Tema #
2.
SECUENCIAS
Y VARIACIÓN
¿Alguna vez te ha
tocado organizar algo en tu casa? ¿Cómo lo has hecho? ¿Qué has tenido en
cuenta?
Así como has respondido
ocurre con los números y figuras. Antes de desarrollar los siguientes
ejercicios te propongo que veas el siguiente video si lo puedes observar. El
Link https://www.youtube.com/watch?v=0frmX-MWMOo
Cuando se ordenan números
o figuras se establece una secuencia. Observa la siguiente situación y léela
hasta comprenderla.
Margarita celebra la
fiesta de su cumpleaños. Antes de que lleguen sus invitados organizará en grupo
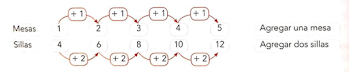
las mesas y las sillas tal como se muestra en el esquema.
·
En el esquema se observa una secuencia donde
cambia el número de objetos de un grupo a otro por cada mesa se agregan dos
sillas.
·
Si se organizan 6 mesas se necesitarán 14
sillas, porque el patrón de cambio es: por cada mesa se agregan dos sillas.
PRACTICA CON TU GUÍA
1.
Identifica el patrón de cambio de cada
secuencia y completa los términos que faltan
El
cambio se expresa cualitativamente cuando
se describe su naturaleza y cuantitativamente
cuando se da valor numérico a las características que varían en cada momento.
El
criterio o regla de cambio se llama patrón
de cambio.
Veamos si captaste este
tema y te pido realices los siguientes ejercicios.
2.
EJERCITACIÓN.
Observa
cada secuencia numérica y establece el patrón de cambio.
|
secuencias |
Patrón de
cambio |
||||
|
3 |
8 |
13 |
18 |
23 |
|
|
25 |
21 |
17 |
13 |
9 |
|
|
2 |
4 |
8 |
16 |
32 |
|
|
81 |
27 |
9 |
3 |
1 |
|
3.
RAZONAMIENTO. Encuentra
los seis primeros términos de cada secuencia de acuerdo con el patrón dado.
|
Patrón de
cambio |
Secuencias |
|||||
|
Sumar 6 |
7 |
13 |
|
|
|
|
|
Restar 9 |
300 |
|
|
|
|
|
|
Multiplicar
por 4 |
2 |
|
|
|
|
|
|
Dividir
por 2 |
800 |
|
|
|
|
|
4.
COMUNICACIÓN.
Dibuja
la siguiente figura de la secuencia en el cuaderno. Establece el patrón de
cambio.
|
Patrón:______________ |
Patrón:______________ |
Solución
de problemas
5.
·
¿Cuántas vallas necesitará para rodear 6
árboles?
·
¿Cuál es el patrón de cambio?
Recuerda
llámame cuando no entiendas algo; estoy para responderte en el horario de 1.00
P.M. a 5: 30 P.M.
AUTOEVALUACIÓN
Después de terminar el estudio con estas guías, realiza las
siguientes preguntas. Sé sincero consigo mismo
1. ¿Fue claro y entendible el contenido en cada
tema? _________________________
2. ¿Los ejemplos que se proporcionaron y los videos
fueron claros para ayudarte a desarrollar los ejercicios propuestos? ________________________________________
3. ¿Necesitaste pedir ayuda para resolver los
ejercicios que se te propusieron? __________________________________________________________
4. ¿En cuál de los temas consideras que te fueron
fácil y entendible? ___________________________________________________________
5. En cual o cuales ejercicios te fueron difíciles
y aún no has entendido. _______________________________________________________________
|
DETENER LA
PROPAGACIÓN DEL COVID 19 ES UN COMPROMISO DE TODOS |
|
|
GUIA DE TRABAJO
EN CASA Área y/o
asignatura: ARITMÈTICA
Grado: 4 Curso:
1, 2, 3. Período Académico: III
FECHA: JULIO 21
AL 21 DE AGOSTO DE 2020 DOCENTE: Elizabeth Navarro
NOMBRE DE LA
UNIDAD: DIVISIÒN DE NÙMEROS NATURALES Y FRACCIONES |
|
|
Propósitos de aprendizajes:
Descompone números en factores primos y
calcula el m.c.m. y el m.c.d. de dos o más números.
Lea, escriba y representa gráficamente
una fracción calcula la mitad, el tercio y cuarta parte de un número.
Reconoce que las fracciones son
indispensables para resolver situaciones cotidianas.
Identifica partes iguales en figuras
que se le plantea. |
Contenidos temáticos: NÙMEROS
PRIMOS Y COMPUESTOS DESCOMPOSICIÒN DE NÙMEROS EN FACTORES
PRIMOS MÌNIMO COMÙN MULTIPLO Y MÀXIMO COMÙN
DIVISOR LA FRACCIÒN Y SUS TÈRMINOS RELACIONES DE ORDEN DE FRCCIONES
HOMOGÈNES Y HETEROGÈNEAS |
Mi Querido Estudiante, recibe un
abrazo bien fuerte de mi parte; demos gracias a Dios por la vida, por nuestra
familia y por la fortaleza y esperanza que Jesús nos da cada día. Te expreso mi
cariño y aprecio que te tengo, por eso cuenta conmigo en el desarrollo de esta
nueva guía. Profe. ELIZABETH NAVARRO
MOMENTO 1. CONOCIMIENTOS PREVIOS
A partir de este momento debes tener a la mano tus implementos
necesarios como son la cartuchera, lapicero, lápiz, colores, implementos
geométricos y tu cuaderno. TODO DEBES PASARLO AL CUADERNO. Además, te invito
mantener una posición cómoda para tu aprendizaje en casa.
En nuestra vida familiar tenemos el árbol genealógico y uno de lo que
los conforma también son los primos. ¿QUIEN ES UN PRIMO? ¿CUÀNTOS PRIMOS
TIENES?
Después de responder estas preguntas te vas a dar cuenta que los
números también tienen primos. Es por eso que a continuación te vas a dar
cuenta cuales son esos números. https://youtu.be/cDmbOJClwi0
MOMENTO 2. CONCEPTUALIZACIÒN
TEMA No.1 NUMEROS PRIMOS Y COMPUESTOS
Según la cantidad de factores o divisores, un número puede ser PRIMO o
COMPUESTO.
Los NÙMEROS PRIMOS son aquellos que solo tienen dos divisores distintos
que son: el 1 y él mismo. Ej.
17 es un número primo porque solo se puede dividir por 1 y por 17
17 entre
1 = 17 y 17 entre 17 = 1
Los NÙMROS COMPUESTOS son los que tienen más de dos divisores Ej.
18 es un
número compuesto porque se puede dividir por 1, 2, 3, 6, 9, y 18
18 entre 1 = 18
18 entre 2 = 9
18 entre 3 = 6
18 entre 6 = 3
18 entre 9 = 2
18 entre 18 = 1
Estos dos conceptos debes tenerlos bien claro para seguir desarrollando
lo que sigues.
Analiza el siguiente ejemplo. Léelo hasta entenderlo, para ello debes
releerlo varias veces.
En una pequeña granja quieren sembrar 18 árboles. Si los ponen en filas
con igual número de árboles. ¿de cuántas maneras distintas los pueden
organizar? Recuerda que los dibujos te ayudan mucho, por eso te pido que lo
hagas.
Vean cómo se resuelve este problema.
Para identificar todas Las
posibilidades, se deben buscar los factores o divisores de 18
18 = 1 X 18 18 = 2 X 9 18 = 3 X
18 es un número compuesto.
R/. Se pueden organizar en filas
de uno, dos, tres, seis, nueve o 18 árboles.
Ahora bien, si se aumenta un árbol, no se pueden organizar por filas
iguales, ya que 19 solamente tiene como divisores el número 1 y él mismo. Así.
19
= 1 X 19
VAS A TENER MUY PRESENTE LO QUE A CONTINUACIÒN VAS A REALIZAR CON EL FÌN
DE QUE TENGAS ÈXITO EN LO QUE SE TE PIDE.
PRACTICA CON LA PERSONA QUE TE COLABORA. ES SUPER FÀCIL.
Vas a encontrar los números primos menores que 100. SIGUE LAS
SIGUIENTES INSTRUCIONES. Puedes usar lápices de colores. Y hacer este cuadro en
una hoja aparte, cuando lo hayas hecho lo pega al cuaderno.
·
Tacha el
número 1, no es primo
·
Encierra
en un círculo el 2, que es el número primo más pequeño.
·
Tacha los
demás números pares.
·
Encierra
en un círculo el 3; tacha sus múltiplos.
·
Encierra
en un círculo el 5; tacha sus múltiplos
·
Encierra
en un círculo el 7; tacha sus múltiplos.
·
Los
veinticinco números que quedan sin tachar son números primos. Escríbelos en el
cuaderno.
MOMENTO 3: APLICA Y RESUELVE
En este momento 3, te invito a
practicar acompañado de la persona que te guía, a comprender y a formalizar el
concepto y a desarrollar tus competencias.
EJERCITACIÒN. Colorea con azul los números primos y con verde los
números compuestos.
22 57 42 49 7 83 36 2 11 15 63 6 5
COMUNICACIÒN. Busca una situación para decir por qué el 1 no es un
número primo ni número compuesto. Debes escribirlo.
.
.
INSTITUCIÓN EDUCATIVA SAN JOSÉ
Resolución de Aprobación N°0746 de junio 12/2009
Nit 812.000.635-2 Dane N° 123001004519
Calle 39 N° 16B -55
Montería - Córdoba
“FORMANDO INTEGRALMENTE LOGRAREMOS
CIUDADANOS COMPETENTES”
TEMA No.2 DESCOMPOSICIÒN EN FACTORES
PRIMOS
Los NÙMEROS COMPUESTOS, se pueden presentar
como un producto de FACTORES PRIMOS
Lea detenidamente el siguiente ejemplo.
Recuerda que si lo relés entenderás lo que más adelante vas a realizar.
Para empacar una colección de música de 18
discos compactos en cajitas y paquetes, se propusieron los siguientes arreglos:
·
Tres
cajas, cada una con tres paquetes, y en cada paquete dos discos. Así:
3 X 3 X 2
·
Tres
cajas, cada una con dos paquetes, y en cada paquete tres discos. Así:
3 X 2 X 3
_____________________________________________________________________________________________
·
Dos cajas, cada una con tres paquetes, y en cada
paquete tres discos. Así 2 X 3 X 3
En los tres casos se descompuso el número
18 en sus factores primos. Observen el dibujo.
https://youtu.be/OGg6Ubplbkw.
En los tres casos se descompuso el número 18 en sus factores primos.
·
Para
descomponer el número 18 en sus factores primos, se hace de la siguiente
manera. Observa paso a paso lo
siguiente.
Deben darse cuenta, que cuando se obtiene 1 en la columna de la
izquierda (paso 3), finaliza el proceso. Los factores primos de 18 son: 2, 3 y
3. Se escribe 18 = 2 X 3 X 3. Son los
números que están en la parte derecha de la línea vertical en el paso 3.
OTRO EJEMPLO YA NO PASO A PASO
Atrévete a practicar
y a desarrollar los siguientes ejercicios. Si analizas los ejercicios
anteriores, puedes darte cuenta qué al multiplicar los números de la derecha
que son primos dan el resultado del número inicial.
DESARROLLA TUS
COMPETENCIAS
1.
Expresa cada número como el producto
de sus factores primos.
2.RAZONAMIENTO. Relaciona cada número con su descomposición en factores
primos. Realiza los cálculos en el cuaderno.
2 X 2 X 3 X 5 90
2 X 3 X 3 X 5 60
3.MODELACIÒN. Otra
forma de hallar los factores primos de un número es mediante el árbol de
factores. Observa el ejemplo y completa el árbol de la derecha
4- SOLUCIÒN NDE
PROBLEMAS
Se requieren exponer
12 mariposas en vitrinas y cuadros, de tal manera que se tenga el mismo número
de cuadros en cada vitrina y el mismo número de mariposas en cada cuadro. ¿Cómo
se pueden organizar las mariposas?
Observa el dibujo y
haz tu lo mismo. Ojalá lo hagas mejor.
Te deseo buena suerte
en todo lo que realices. Recuerda que estoy para ayudarte. Llámame cuando lo
desees.
TEMA No, 3
Recuerdas que significa: ¿múltiplo de un número? En la guía pasada lo
vimos. Te recomiendo volver a ella y refrescar el concepto. A continuación, vas
a encontrar otro contenido referente a la aplicación de lo que ya conoces.
MÌNIMO COMÙN MÙLTIPLO
El mínimo común múltiplo (m.c.m.) de dos o más números es el menor de
los múltiplos comunes, diferentes de cero.
Esto es supremamente sencillo, sigue el ejemplo que te presento.
Hallar el mínimo común múltiplo de 3 y 6.
Te explico. Primero hallamos los múltiplos de 3 y de 6. Como lo
aprendiste en la guía anterior.
Múltiplo de 3 = (0, 3, 6, 9, 12, 15, 18, 21, 24,27, 30…)
Múltiplo de 6 = (0, 6, 12,18,24, 30…)
Después nos damos cuenta, cuáles son los múltiplos comunes, esto quiere
decir los números que están en 3 y en 6.
Veamos, el conjunto de múltiplos comunes de 3 y 6 son: (0, 6, 12, 18,
24, 30…)
Entonces vemos cual es el número menor, y ese es el m.c.m. (3, 6) = 6.
Dicho de otra forma, el número menor de 3 y de 6, es el número 6
OTRO EJEMPLO
Hallar cuatro múltiplos comunes de 5 y 15.
Seguimos las instrucciones del ejemplo anterior.
Múltiplos de 5 = (0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65,
70, …)
Múltiplos de 15 = (0, 15, 30, 45, 60, 75, 90, 105,120, …)
R/. Los cuatros múltiplos comunes de 5 y 15 son: 15, 30, 45 y 60
https://youtu.be/txLlA_fyL5g
APLICA Y RESUELVE
Teniendo en cuenta la explicación anterior, desarrollo los siguientes
ejercicios
1.
MODELACIÒN. Escribe los diez
primeros múltiplos de cada número y establece el menor múltiplo común
Múltiplo de 4 =
Múltiplo de 5 =
Múltiplo de 4 y 5 =
m.c.m. (4, 5) =
2.
EJERCITACIÒN. Utiliza la
descomposición en factores primos para hallar el mínimo común múltiplo de cada
grupo de número. Realiza en el cuaderno.
a) m.c.m. (4 y 6)
b) m.c.m. (4, 6, y 9)
3.
SOLUCIÒN DE PROBLEMA.
Un ciclista tarda dos minutos en dar una
vuelta a la pista y otro tarda tres minutos. Si parten al mismo tiempo y deben
dar 50 vueltas, ¿cuántas veces se encontrarán en el punto inicial? ¡cuantos
minutos hay entre cada encuentro?
Te recomiendo representar el dibujo, además
concentrarte en la pregunta que te presenta el problema. Suspira, relájate, haz
un ejercicio y luego continúa tu trabajo
TEMA No. 4
El contenido de este tema va de la mano de
lo que ya conoces como divisores de un número, es por esto que podrías sacar
una conclusión, sobre la secuencia de los temas que has venido aprendiendo y
realizando. ¿Qué son los divisores de un número? Responde en tu cuaderno. TODO
DEBE ESTAR ESCRITO EN EL CUADERNO.
MÀXIMO COMÙN DIVISOR
El MÀXIMO COMÙN DIVISOR (m.c.d.) de dos o
más números es el mayor de los divisores comunes.
Veamos cómo se hace.
LO PRIMERO ES BUCAR LOS DIVISORES DE CADA
NÙMERO
LO SEGUNDO ES VER CUALES SON LOS NÙMEROS
COMUNES Y
LO TERCERO ES SELECCIONAR EL NÙMERO COMÙN
MÀS GRNDE DE LOS DOS NÙMEROS, Ejemplos
1. Hallar el m.c.d. de 18 y 24
Divisores de 18 =
(1, 2, 3, 6, 9, 18)
Divisores de 24 =
(1, 2, 3, 4, 6, 8, 24)
El conjunto de
divisores comunes de 18 y 24 es: (1, 2, 3, 6)
El máximo común
divisor de 18 y 24 es = 6
2. Hallar el m.c.d. de 15 y 25
Divisores de 15 = (1, 3, 5, 15)
Divisores de 25 = (1, 5, 25)
El conjunto de divisores comunes de 15 y 25
es = (1, 5)
El máximo común divisor de 15 y 25 es = 5
https://youtu.be/WD4rGWCRBYY
APLICA Y RESUELVE
Demuestra que entendiste los ejercicios
anteriores y ahora te corresponde desarrollar los siguientes.
EJERCITACIÒN. Escribe los divisores de cada
número y establece el mayor divisor común.
1. Hallar el m.c.d. de 12 y 18
Divisores de 12 =
Divisores de 18 =
Divisores comunes de 12 y 18 =
m.c.d. de 12 y 18 =
2. Halla el m.c.d. de 12, 16 y 28
Divisores de 12 =
Divisores de 16 =
Divisores de 28 =
Divisores comunes de 12, 16, 18 =
m.c.d.
RAZONAMIENTO. Marca el recuadro con el
máximo común divisor, según el caso.
m.c.d. (12, 24) ------------------------------ 12 4 2
m.c.d.(25, 30,
45)----------------------------- 10 2 5
m.c.d.(8, 16, 24)
------------------------------ 8 4 2
SOLUCIÒN DE PROBLEMAS
Se tienen dos trozos de telas. Uno mide 160
centímetro de largo, y el otro, 120 centímetro. Si se quiere obtener pañuelos
iguales de la mayor longitud posible, sin desperdiciar tela, ¿qué longitud
deben tener los pañuelos?
Te recomiendo utilizar un trozo de tela si
lo tienes, si no forma el pañuelo con papel; te queda fácil para darle
respuesta a la pregunta formulada.
Tú tienes la oportunidad de
avanzar en medio de esta dificultad en la que vivimos.
¡ÀNIMO!
TEMA No. 4
Seguramente, te habrás dado cuenta que cuando vas a una reunión de
cumpleaños; te brindan torta y recibes una porción de la cual quisieras que te
volvieran a dar otro pedazo. ¡Qué rico! Dibuja en tu cuaderno una fiesta de
cumpleaños y en el centro una torta ya partida, Demuestra tu creatividad,
dibuja los invitados y todo lo que quieras representar.
A continuación, vamos a estudiar, partiendo de la torta grande que
había en el cumpleaños y la dividieron entre los invitados. Esto representa una
clase de números que se llaman NÙMEROS FRACCIONARIOS
Cómo puedes definir: ¿Qué son números fraccionarios? Responde en tu
cuaderno
NÙMEROS FRACCIONARIOS
FRACCIONES
Y SUS TERMINOS
Una fracción
se representa matemáticamente por números que están escritos uno
sobre otro y que se hallan separados por una línea recta horizontal llamada
raya fraccionaria.
La fracción está formada por dos términos:
el numerador y
el denominador. El numerador es el número que está sobre la raya
fraccionaria y el denominador es el que está bajo la raya fraccionaria.
FRACCIONES HOMOGENEAS Y HETEROGENEAS
Llamamos fracciones homogéneas a aquellas que
comparten el mismo denominador por ejemplo
Dos fracciones son heterogéneas cuando estas poseen
distinto denominador, por ejemplo:
Fracciones
equivalentes: qué son y cómo calcularlas
Vamos
a aprender qué son las fracciones equivalentes.
Son
aquellas fracciones que representan la misma cantidad.
La
primera figura está dividida en dos partes y hemos coloreado una de ellas. Por
lo tanto, su fracción será 1/2.
La
segunda figura la hemos dividido en 4 partes y hemos coloreado dos. Por lo tanto,
su fracción será 2/4.
Y la
tercera figura la hemos dividido en 6 partes y hemos coloreado 3, por lo que su
fracción será 3/6.
Si te
fijas la parte coloreada en todas las figuras es la misma, aunque las
fracciones son diferentes.
Te
recomiendo los siguientes videos: https://youtu.be/c9cTIjBqFTw
SOLUCIÒN DE PROBLEMA
Una pizza se dividió en ocho partes iguales. Enrique tomó tres pedazos
y Jimena dos.
·
Expresa
en fracción la cantidad que tomo cada niño.
·
¿Cuántas
raciones quedaron?
AUTOEVALUACIÒN
Al desarrollar esta guía, es recomendable hacer una autoevaluación con
el propósito de reconocer que has aprendido y que te ha quedado por aprender en
estos temas. Por tal razón te invito a que responda con sinceridad las
siguientes preguntas.
¿Ha sido claro, entendible y con un vocabulario acorde a tu edad el
contenido de cada tema?
-------------------------------------------------------------------------------------------------------------------------------------------
¿Los ejercicios que se te proporcionaron, al igual que los videos
fueron aportes para ayudarte a realizar las actividades?
--------------------------------------------------------------------------------------------------------------------------------------------
¿Necesitaste de alguien que te ayudara para resolver los ejercicios y
recibiste con humildad lo que te explicaba?
----------------------------------------------------------------------------------------------------------------------------------------------
¿Cuál de los temas te gustó más y cómo puedes aplicarlo a tu vida?
-----------------------------------------------------------------------------------------------------------------------------------------------
¿En cuál de los temas necesitas afianzar más? ¿Porque no lo has
entendido?
-----------------------------------------------------------------------------------------------------------------------------------------------
Resolución de Aprobación N°0746 de junio 12/2009
Nit 812.000.635-2 Dane N° 123001004519
Calle 39 N° 16B -55
Montería - Córdoba
“FORMANDO INTEGRALMENTE LOGRAREMOS CIUDADANOS
COMPETENTES”
|
DETENER LA
PROPAGACIÓN DEL COVID 19 ES UN COMPROMISO DE TODOS |
|
|
GUIA DE TRABAJO
EN CASA Área y/o
asignatura: GEOMETRÌA
Grado: 4 Curso:
1, 2, 3.
Período Académico: III FECHA: JULIO 21
AL 21 DE AGOSTO DE 2020 DOCENTE:
Elizabeth Navarro NOMBRE DE LA
UNIDAD: UNIDADES DE ÀREA |
|
|
Propósitos de aprendizajes:
Realiza cálculos y mediciones de figuras tales
como: cuadrado, rectángulo, triángulos que hay en su entorno. Reconoce situaciones que requieren de la
medición, haciendo uso de fórmulas universales. |
Contenidos temáticos: Concepto
de área Área del cuadrado, rectángulo y del
triángulo |
Mi querido estudiante.
Cordial saludo, con mucho cariño y respeto. Dios todopoderoso, los lleve en sus
brazos en estos momentos tan estresantes y los colme de mucha sabiduría y
bendiciones. Cuente con mi apoyo en todo lo que te toca realizar, siempre estoy
presta para escucharte.
Tú profesora. Elizabeth
Navarro.
MOMENTO 1.
CONOCIMIENTOS PREVIOS
Mira a tu alrededor y comenta que figuras
geométricas observa; encuéntralas y dibújalas en tu cuaderno, haz buen uso de
la regla y demás implementos geométricos.
Te recuerdo que desde ya puedes hacer
buen uso de tus habilidades para representar las figuras que desees, debes
colorearlas y te recomiendo que al utilizar el color haz buen uso de éste sin
salirte del contorno, hazlo en una misma dirección con el fin de que te quede
con buena presentación.
https://youtu.be/TZDgCnfDrIE 1
Momento 2. CONCEPTUALIZACIÒN
UNIDADES
DE AREA
El concepto de área
se refiere a un espacio de tierra que se encuentra comprendido entre ciertos
límites. En este sentido, un área es un espacio delimitado por determinadas
características geográficas, zoológicas, económicas o de otro tipo.
Existen otros muchos
tipos de áreas que se convierten en parte de nuestro día a día. Así, por
ejemplo,
nos encontramos con las llamadas áreas de descanso (casa, piscina, finca,
hotel, etcétera).
Para la geometría, un área es la superficie comprendida dentro de un perímetro, que
se expresa en unidades de medidas que son conocidas como superficiales. Existen
distintas fórmulas para calcular el área de las diferentes figuras, como los
triángulos, los cuadrados y los rectángulos.
Para medir una superficie de una
figura se elige un cuadrado como unidad y se recubre la figura con dicho
cuadrado. El número de veces que la figura contiene el cuadrado es el área de
esa figura.
La unidad fundamental de medida de
superficie es el metro cuadrado (m2) El decímetro cuadrado y el
centímetro cuadrado son unidades de medida de superficie menores que el metro
cuadrado.
AREA
DE FIGURAS PLANAS:
En esta clase vamos a ver el área de algunas
figuras planas, estudiaremos el triángulo, rectángulo y el cuadrado. El área es
una medida de extensión de una superficie, expresada en unidades de medida denominadas
unidades de superficie
Área del
triángulo
El área de un triángulo es igual
al semiproducto de la base por su altura, es decir.
A= área
b= base
h= altura
Ejemplo: Calcular el área del triángulo de las figuras
1)
2)
A
=
Área del rectángulo
El área del rectángulo es igual al producto de la base por
la altura, es decir.
A = b
x h
b = base
h = altura
Ejemplo: Calcular el área del rectángulo de las figuras.
1)
b = 12 cm
A = 12 x 8 = 96 cm2
h = 8 cm
4cm A = 13x4 = 52 cm2
13cm
Área del cuadrado
El área del cuadrado es igual al
producto de lado por lado, es decir.
A = L
x L = L2
A = área: L= lado
Ejemplo:
Calcular el área del cuadrado de las siguientes figuras.
A=?
L = 7 dm
A = 7x7 = 49 dm2
A =?
L= 13
cm
A =
13x13 = 169 cm2
13 cm
Momento
3: APLICA Y RESUELVE
1) Observa estas figuras. ¿Cuál tiene mayor
superficie?..........Ordénalas de mayor a menor.
2) Calcula en área de cada figura usando como
unidad el cuadrado de la cuadrícula.
3)
Completa
las siguientes letras, coloréalas y escribe debajo su área.
4) Calcula
el área de las siguientes figuras planas.
1)
2)
3)
4cm
8 cm
AUTOEVALUACIÒN
Al terminar de
desarrollar este tema quiero escuchar tu apreciación sobre lo que acabas de
hacer. Como siempre les digo, uno mismo no debe engañarse, hay que ser sincero
en lo que haces.
¿Aprendiste el concepto
de área y lo puedes asociar con lo que te rodea?
------------------------------------------------------------------------------------------------------------------------
Si te pregunto. ¿Cuál
es el área de la mesa de tu comedor, cómo me respondes? ¿Dime que tienes que
hacer?
-----------------------------------------------------------------------------------------------------------------------------
¿Para qué te sirve el
contenido aprendido? ¿Cómo lo aplicarías en tu vida?
-----------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------
Aprendiste el uso de las
fórmulas para hallar el área de; ¿cuadrado, rectángulo y triángulo? ¿O se te
dificulta?
------------------------------------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------------------------------------
Resolución de Aprobación N°0746 de junio 12/2009
Nit 812.000.635-2 Dane N° 123001004519
Calle 39 N° 16B -55
Montería - Córdoba
“FORMANDO INTEGRALMENTE LOGRAREMOS CIUDADANOS
COMPETENTES”
|
DETENER LA
PROPAGACIÓN DEL COVID 19 ES UN COMPROMISO DE TODOS |
|
|
GUIA DE TRABAJO
EN CASA Área y/o
asignatura: ESTADISTICA
Grado: 4 Curso:
1, 2, 3. Período
Académico: III FECHA: JULIO 21
AL 21 DE AGOSTO DE 2020 DOCENTE:
Elizabeth Navarro NOMBRE DE LA
UNIDAD: VARIACIÒN |
|
|
Propósitos de aprendizajes:
Describe e interpreta variaciones representado en gráficas |
Contenidos temáticos: El cambio y la variación |
Querido estudiante; dejemos la prisa,
los afanes por entregar a las carreras estas guías y, de cualquier manera, sin
antes haber realizado un trabajo minucioso, entiendan que las actividades que
les propongo son entendibles, debes leer y releer. El tiempo de Dios es
perfecto para su entrega. Te quiero mucho.
Profe.
Elizabeth Navarro
MOMENTO 1. CONOCIMIENTOS PREVIOS
Responde las siguientes preguntas con
base en lo que has aprendido en temas anteriores.
1.
¿Qué debes tener en cuenta para hacer
una gráfica?
2.
¿Para qué sirven las gráficas?
3.
¿Sabes leer las gráficas?
4.
De las gráficas estudiadas hasta
ahora. ¿Cuál te ha sido más fácil y cuál te ha gustado más? ¿Porqué?
T E RECOMOENDO ESTE VIDEO PARA QUE
OBSERVES COMO HACER UN DIAGRAMA DE LÌNAS
Si tienes la oportunidad de observarlo
el link es https://youtu.be/dHAjU1VIaSg
MOMENTO 2. CONCEPTUALIZACIÒN
REPRESENTACIÒN GRÀFICA DEL CAMBIO
Para representar el cambio en una
situación, se puede usar una gráfica de puntos.
Te explico; como se ha venido
observando a través de la pandemia, se dan a conocer resultados usando las
gráficas y de esta manera los estudiosos pueden tomar decisiones de acuerdo a
los resultados que se han venido dando.
Lo anterior nos indica que a partir
de la representación gráfica del cambio se puede obtener información importante
sobre cómo evoluciona determinada situación y tomar decisiones.
A continuación, te presento la
siguiente situación léela y reléela para tu comprensión.
Héctor vende periódicos en un kiosko.
Para llevar la contabilidad de su negocio, registra en una tabla la cantidad de
periódicos que vende cada día.
La información de la tabla se puede
representar en una gráfica de puntos.
¿Cómo se hace?
·
Se trazan dos rectas perpendiculares.
·
En el eje horizontal se ubican los
días, y en el eje vertical la cantidad de periódicos vendidos.
·
Se ubican las parejas ordenadas.
A PARTIR DE LA GRÀFICA SE PUEDE
CONCLUIR:
-
El lunes es el día que menos
periódicos vende.
-
Durante los tres primeros días, el
número de periódicos siempre aumentó.
-
Entre el miércoles y el jueves el
número de periódicos vendidos se mantuvo.
-
El sábado fue el día de mayor venta.
MOMNTO 3. APLICA Y RESUELVE
1.
Completa la tabla de acuerdo con la
información dada en la gráfica.
2.
EJERCITACIÒN. La gráfica que a
continuación te presento, muestra la cantidad de dinero que gasta una persona
durante quince días.
·
¿Cuánto dinero gastó durante los
primeros siete días?
·
¿Qué días gastó la misma cantidad de
dinero?
·
¿Qué días gastó más dinero?
·
¿Qué día gastó menos dinero?
·
¿Qué título tiene la gráfica?
·
¿Qué datos se ubican en la línea
horizontal?
·
¿Qué datos se ubican en el eje
vertical?
·
Une los puntos y verás como queda la gráfica
de línea
·
Haz esta gráfica en tu cuaderno, que
te ocupe más de la mitad de la hoja.
Te recuerdo, utilizar la regla para que te quede bien
elaborada. Los puntos puedes hacerlo a color.
3.
SOLUCIÒN DE PROBLEMAS,
Consigue el recibo del agua de tu casa. Analiza los diagramas
de evolución de consumo, elabora la gráfica de puntos correspondiente y
contesta.
·
¿En qué mes se consumió más agua?
·
¿En qué mes se consumió menos agua?
·
¿Hay algunos meses que presentan el
mismo consumo?
·
Dale una idea a tus padres, para que
cuando ya se normalice la pandemia, disminuir el consumo de agua y ponerla en
práctica. Recordemos que el agua es un recurso natural, muy valioso e
indispensable para la vida.
Nota: Una vez más reitero lo importante que eres para mí y por
lo tanto quiero que realices todas las actividades con dedicación y esmero.
Llámame cuando te sientas confundido, Recuerda el horario de atención los días
hábiles de 1:00 P. M. a 5:30 P.M.
AUTOEVALUACIÒN
Al terminar de realizar estas
actividades, es necesario que te hagas una evaluación con el fin de reconocerte
a Ti mismo de las capacidades que posees y lograrás alcanzar éxito en tu
aprendizaje en casa. Que se reflejará a lo largo de tu vida. Respóndete las
siguientes preguntas.
·
Fuiste
disciplinado en el desarrollo de la guía.
------------------------------------------------------------------------------------------------------------------
·
En este estilo
de clases que te ha tocado vivir en casa, ¿sientes que has aprendido nuevos
contenidos?
----------------------------------------------------------------------------------------------------------------------
·
¿Seguiste
las orientaciones dadas en los encuentros sincrónicos?
--------------------------------------------------------------------------------------------------------------------------
·
¿Has sido
obediente en el uso del micrófono en los encuentros sincrónicos?
---------------------------------------------------------------------------------------------------------------------------
·
¿Sabes
utilizar correctamente la regla en la elaboración de gráficas y figuras
geométricas?
----------------------------------------------------------------------------------------------------------------------------
·
¿Realizaste
las actividades en el cuaderno, y lo mantienes limpio y organizado?
·
¿Escribes
los temas que te sabes y te fueron fáciles?
----------------------------------------------------------------------------------------------------------------------------
·
Anotas
los temas que te falta por aprender, porque no lo has entendido.
----------------------------------------------------------------------------------------------------------------------------















































soy santiago paez y ya hice las actividades de matematica
ResponderEliminarhola soy nicol londoño y ya termine mais actividades de matematicas😊
ResponderEliminarhola soy nicoll londoño ya termine las actividades de estadistica
ResponderEliminarHola soy sharik puentes y lla termine la tarea de matemáticas
ResponderEliminarhola soy nicol londoño y ya termine las actividades de geometria
ResponderEliminarHola soy sharik puentes y lla termine la tarea de matemáticas
ResponderEliminar